Forecasting statistics for golf betting

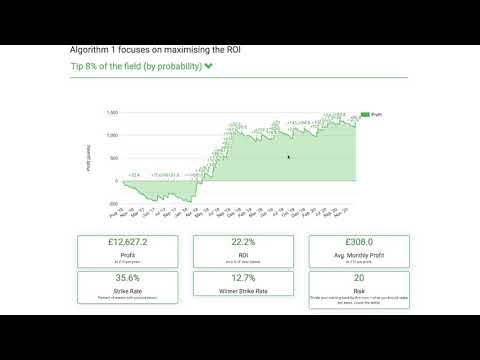
Thanks to websites and podcasts specializing in golf betting content, knowing the golf stats that matter each week has gotten increasingly easier for bettors. Using Historical Data and Analytics for Better Predictions: The past can inform the forecasting statistics for golf betting. By leveraging databases of player performances. Golf Forecast is an innovative betting service that uses an algorithm to generate selections. It performed very well during our extended seven. That included Masters odds for the entire field of 90+ golfers, the results of every PGA and LIV Golf event from the past 12 months, and a.

How Do Golf Odds Work?

Ultimately I do think this is the way to go if you want to incorporate course fit: if you had detailed course data perhaps about average fairway width, length, etc. Unfortunately in our case, with the course variables we used, it was again mostly a noise mine.

This has left us thinking that there is not an effective way to systematically incorporate course fit into our statistical models. The sample sizes are too small, and the measures of course similarity to crude, to make much headway on this problem. That's not to say that course history doesn't exist; it probably does. But to separate the signal from the noise is very hard.

Given the analysis and discussion so far, we can now think of having a set of models to choose from where differences between models are defined by a few parameters. These parameters are the choice of weighting scheme on the historical strokes-gained averages this involves just a single parameter that determines the rate of exponential decay moving backwards in time , and also the weights that are used to incorporate the detailed strokes-gained categories through a reweighting method.

The optimal set of parameters are selected through brute force: we loop through all possible combinations of parameters, and for each set of parameters we evaluate the model's performance through a cross validation exercise. This is done to avoid overfitting: that is, choosing a model that fits the estimating data very well but does not generalize well to new data.

The basic idea is to divide your data into a "training" set and a "testing" set. The training set is used to estimate the parameters of your model for our model, this is basically just a set of regression coefficients [9] , and then the testing set is used to evaluate the predictions of the model. We evaluate the models using mean-squared prediction error, which in this context is defined as the difference between our predicted strokes-gained and the observed strokes-gained, squared and then averaged.

Cross validation involves repeating this process several times i. This repetitive process is again done to avoid overfitting. The model that performs the best in the cross validation exercise should hopefully be the one that generalizes the best to new data. That is, after all, the goal of our predictive model: to make predictions for tournament outcomes that have not occurred yet.

One thing that becomes clear when testing different parameterizations is how similar they perform overall despite disagreeing in their predictions quite often. This is troubling if you plan to use your model to bet on golf. For example, suppose you and I both have models that perform pretty similar overall i. This means that both of our models would find what we perceive to be "value" in betting on some outcome against the other's model.

However, in reality, there is not as much value as you think: roughly half of those discrepancies will be cases where your model is "incorrect" because we know, overall, that the two models fit the data similarly. Forecasting statistics for golf betting The model that we select through the cross validation exercise has a weighting scheme that I would classify as "medium-term": rounds played years ago do receive non-zero weight, but the rate of decay is fairly quick.

Compared to our previous models this version responds more to a golfer's recent form. In terms of incorporating the detailed strokes-gained categories, past performance that has been driven more by ball-striking, rather than by short-game and putting, will tend to have less regression to the mean in the predictions of future performance.

To use the output of this model — our pre-tournament estimates of the mean and variance parameters that define each golfer's scoring distribution — to make live predictions as a golf tournament progresses, there are a few challenges to be addressed. First, we need to convert our round-level scoring estimates to hole-level scoring estimates.

This is accomplished using an approximation which takes as input our estimates of a golfer's round-level mean and variance and gives as output the probability of making each score type on a given hole i. Second, we need to take into account the course conditions for each golfer's remaining holes. For this we track the field scoring averages on each hole during the tournament, weighting recent scores more heavily so that the model can adjust quickly to changing course difficulty during the round.

Of course, there is a tradeoff here between sample size and the model's speed of adjustment. Another important detail in a live model is allowing for uncertainty in future course conditions. This matters mostly for estimating cutline probabilities accurately, but does also matter for estimating finish probabilities.

If a golfer has 10 holes remaining, we allow for the possibility that these remaining 10 holes play harder or easier than they have played so far due to wind picking up or settling down, for example. We incorporate this uncertainty by specifying a normal distribution for each hole's future scoring average, with a mean equal to it's scoring average so far, and a variance that is calibrated from historical data [10].

The third challenge is updating our estimates of player ability as the tournament progresses. This can be important for the golfers that we had very little data on pre-tournament. For example, if for a specific golfer we only have 3 rounds to make the pre-tournament prediction, then by the fourth round of the tournament we will have doubled our data on this golfer!

Updating the estimate of this golfer's ability seems necessary. 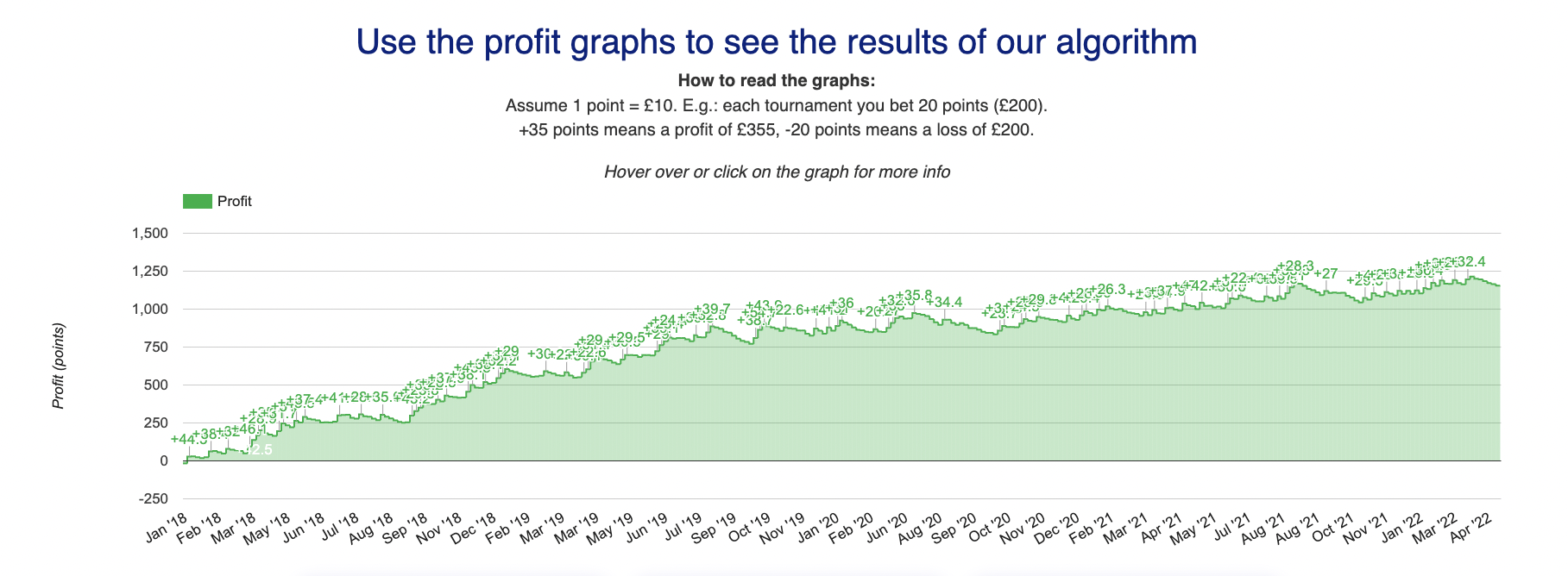To do this, we have a rough model that takes 4 inputs: a player's pre-tournament prediction, the number of rounds that this prediction was based off of, their performance so far in the tournament relative to the appropriate benchmark , and the number of holes played so far in the tournament. The predictions for golfers with a large sample size of rounds pre-tournament will not be adjusted very much: a 1 stroke per round increase in performance during the tournament translates to a 0.

However, for a very low data player, the ability update could be much more substantial 1 stroke per round improvement could translate to 0. With these adjustments made, all of the live probabilities of interest can be estimated through simulation. For this simulation, in each iteration we first draw from the course difficulty distribution to obtain the difficulty of each remaining hole, and then we draw scores from each golfer's scoring distribution taking into account the hole difficulty.

The clear deficiency in earlier versions of our model was that no course-specific elements were taken into account. That is, a given golfer had the same predicted mean i. After spending a few months slumped over our computers, we can now happily say that our model incorporates both course fit and course history for PGA Tour events.

For European Tour events, the model only includes course history adjustments. Further, we now account for differences in course-specific variance, which captures the fact that some courses have more unexplained variance e. TPC Sawgrass than others e. This will be a fairly high-level explainer.

We'll tackle course fit and then course-specific variance in turn. The approach to course fit that was ultimately successful for us was, ironically, the one we described in a negative light a year ago. For each PGA Tour course in our data we estimate the degree to which golfers with certain attributes under or over-perform relative to their baselines where a golfer's baseline is their predicted skill level at a neutral course.

The attributes used are driving distance, driving accuracy, strokes-gained approach, strokes-gained around-the-green, and strokes-gained putting. More concretely, we correlate a golfer's performance i. Attribute-specific skill levels are obtained using analogous methods to those which were described in an earlier section to obtain golfers' overall skill level.

For example, a player's predicted driving distance skill at time t is equal to a weighted average of previous adjusted for field strength driving distance performances, with more recent rounds receiving more weight, and regressed appropriately depending on how many rounds comprise the average.

The specific weighting scheme differs by characteristic; not suprisingly, past driving distance and accuracy are very predictive of future distance and accuracy, and consequently relatively few rounds are required to precisely estimate these skills. Conversely, putting performance is much less predictive, which results in a longer-term weighting scheme and stronger regression to the mean for small samples.

With estimates of golfer-specific attributes in hand, we can now attempt to estimate a course-specific effect for each attribute on performance — for example, the effect of driving distance on performance relative to baseline at Bethpage Black. The main problem when attempting to estimate course-specific parameters is overfitting. Despite what certain sections of Golf Twitter would have you believe, attempting to decipher meaningful course fit insights from a single year of data at a course is truly a hopeless exercise.

This is true despite the fact that a year's worth of data from a full-field event yields a nominally large sample size of roughly rounds. Performance in golf is mostly noise, so to find a predictive signal requires, at a minimum, big sample sizes it also requires that your theory makes some sense.

To avoid overfitting, we fit a statistical model known as a random effects model. It's possible to understand its benefits without going into the details. Consider estimating the effect of our 5 attributes on performance-to-baseline separately for each course: it's easy to imagine that you might obtain some extreme results due to small sample sizes. Conversely, you could estimate the effect of our 5 golfer attributes on performance-to-baseline by pooling all of the data together: this would be silly as it would just give you an estimate of 0 for all attributes as we are analyzing performance relative to each golfer's baseline, which has a mean of zero, by definition.

The random effects model strikes a happy medium between these two extremes by shrinking the course-specific estimates towards the overall mean estimate, which in this case is 0. This shrinkage will be larger at courses for which we have very little data, effectively keeping their estimates very close to zero unless an extreme pattern is present in the course-specific data.

Here is a nice interactive graphic and explainer if you want more intuition on the random effects model. Switching to this class of model is one of the main reasons our course fit efforts were more successful this time around. What are the practical effects of incorporating course fit. While in general the difference between the new model, which includes both course fit and course history adjustments, and the previous one which we'll refer to as the baseline model are small, there are meaningful differences in many instances.

If we consider the differences between the two models in terms of their respective estimated skill levels i. I can't say I ever thought there would come a day when we would advocate for a 1 stroke adjustment due to course fit. And yet, here we are. Let's look at an example: before the Mayakoba Classic at El Camaleon Golf Club, we estimated Brian Gay to be 21 yards shorter off the tee and 11 percentage points more accurate in fairways hit per round than the PGA Tour average.

This made Gay an outlier in both skills, sitting at more than 2 standard deviations away from the tour mean. American century classic leaderboard Furthermore, El Camaleon is probably the biggest outlier course on the PGA Tour, with a player's driving accuracy having almost twice as much predictive power on performance as their driving distance there are only 11 courses in our data where driving accuracy has more predictive power than distance.

Therefore, at El Camaleon, Gay's greatest skill accuracy is much more important to predicting performance than his greatest weakness distance. Further, Gay had had good course history at El Camaleon, averaging 1. It's worth pointing out that we estimate the effects of course history and course fit together, to avoid 'double counting'.

That is, good course fit will often explain some of a golfer's good course history. Taken together, this resulted in an upward adjustment of 0. When evaluating the performance of this new model relative to the baseline model, it was useful to focus our attention on observations where the two models exhibit large discrepancies.

The correlation between the two models' predicted skill levels in the full sample is still 0. However, by focusing on observations where the two models diverge substantially, it becomes clear that the new model is outperforming the baseline model. As previously alluded to, the second course-specific adjustment we've made to our model is the inclusion of course-specific variance terms.

This means that the player-specific variances will all be increased by some amount at certain courses and decreased at others. It's important to note that we are concerned with the variance of 'residual' scores here, which are the deviations in players' actual scores from our model predictions this is necessary to account for the fact that some courses, like Augusta National, have a higher variance in total scores in part because there is greater variance in the predicted skill levels of the players there.

All else equal, adding more unexplained variance — noise — to scores will bring the model's predicted win probabilities for the tournament, for player-specific matchups, etc. That is, Dustin Johnson's win probability at a high residual -variance course will be lower than it is at a low-variance course, against the same field. In estimating course-specific variances, care is again taken to ensure we are not overfitting.

Perhaps surprisingly, course-specific variances are quite predictive year-over-year, leading to some meaningful differences in our final course-specific variance estimates. A subtle point to note here is that a course can simultaneously have high residual variance and also be a course that creates greater separation amongst players' predicted skill levels.

For example, at Augusta National, golfers with above-average driving distance, who tend to have higher baseline skill levels, are expected to perform above their baselines; additionally, Augusta National is a course with above-average residual variance. Therefore, whether we would see the distribution of win probabilities narrow or widen at Augusta relative to a typical PGA Tour course will depend on which of these effects dominates.

There are a few important changes to the model. First, we are now incorporating a time dimension to our historical strokes-gained weighting scheme. This was an important missing element from earlier versions of the model. For example, when Graham DeLaet returned in early after a 1-year hiatus from competitive golf, our predictions were mostly driven by his data from and earlier, even after DeLaet had played a few rounds in It seems intuitive that more weight should be placed on DeLaet's few rounds from given the absence of data compared to a scenario where he had played a full season.

Using a weighting function that decays with time e. However, continuing with the DeLaet example, there is still lots of information contained in his pre rounds. Therefore we use an average of our two weighted averages: the first weights rounds by the sequence in which they were played, ignoring the time between rounds, while the second assigns weights based on how recently the round was played.

In DeLaet's case, if he were playing this week Jan 4, , his time-weighted predicted strokes-gained would be Ultimately we combine these two predictions and end up with a final prediction of The difference between this value and the sequence-weighted average is what appears in the "timing" column on the skill decomposition page.

Using strokes-gained, proximity, and GIR to break down approach skill across 6 yardage buckets. Historical Event Tournament Stats. Are certain skill sets — such as distance, or accuracy — favoured at specific courses. Course History Tool. Forecasting statistics for golf betting Detailed player histories as well as suggested adjustments for a golfer's course history and experience.

SG Strokes-Gained Distributions. Ranking and visualizing the round-level distribution of strokes-gained. Who plays best and worst. Letzig's Latest. Our weekly newsletter, delivered to your inbox every Wednesday morning. Read the latest issue.

Bet Tracker. Current Week Past Results. API Access. Statistical modeling helps solve this problem by simplifying the outcomes. Suppose all golfers have scores independent of different courses. Hence, it becomes easy to predict tournament outcomes on its own. Using it helps to make your golf betting headaches less severe, especially for winners of contests.

The rising influx of bettors for golf tournaments is not because it has higher excitement than any regular NFL Sunday game. More players are coming in thanks to the live betting opportunities it provides. This includes an all-year schedule, long shots, and other analytics. Here are some forecasting techniques modern bettors use to determine the final winner.

Remember that no method guarantees accuracy, especially as golf can be unpredictable. Hence, combining them, following pro tipsters, and checking relevant news are important to stay ahead of the competition. Utilizing cutting-edge techniques in predicting sports outcomes enhances accuracy, aids strategic decision-making, and offers a competitive edge in the realm of sports analysis and betting.

ML helps build algorithms that analyze several data types to ensure better predictions. Some of the features it considers are player statistics, form, scores, weather conditions, and course character. Other tools like gradient boosting, decision trees, and similar options can help make the algorithm more effective.

This tool uses historical data from past performances to drive an outcome forecast. Among them are statistics like putting and driving accuracy, with average scoring to set up trends or patterns. Social media, interviews, and news outlets are part of the sentiment technique. In the end, it can forecast the performance of a tournament. It also uses public opinion to create its analysis.

Besides golf betting, neural networks have become a popular analysis tool for several sports. It learns patterns by studying huge amounts of data. These statistics include the history of a particular tournament, player performance, weather factors, and other external features.

It can help build a strong time series analysis. The importance of using statistics when filling out your golf bet slip is often underestimated. They provide undiluted information for different players, using past performance in any tournament to determine the future outing. Bettors can use statistics to place two golfers side-by-side and compare their performances.

This includes considering the strengths and weaknesses of each player.